原文授權轉載自ACGdoge

雖然很多人都說數學只要學加減乘除就夠了,其實這個說法是有問題的,高中和大學的數學知識確實在日常生活中很少用到,但在建築、測量、概率各領域都是重要的基礎知識,就像分析選舉票數也要用上高中以及部分大學數學知識
日本就有人以高中數學的對數以及大學的概率學知識,用數學分析《偶像大師灰姑娘女孩》第6次總選舉的票數情況,並從中提出了想要自己喜歡的偶像進入Top 50的方法
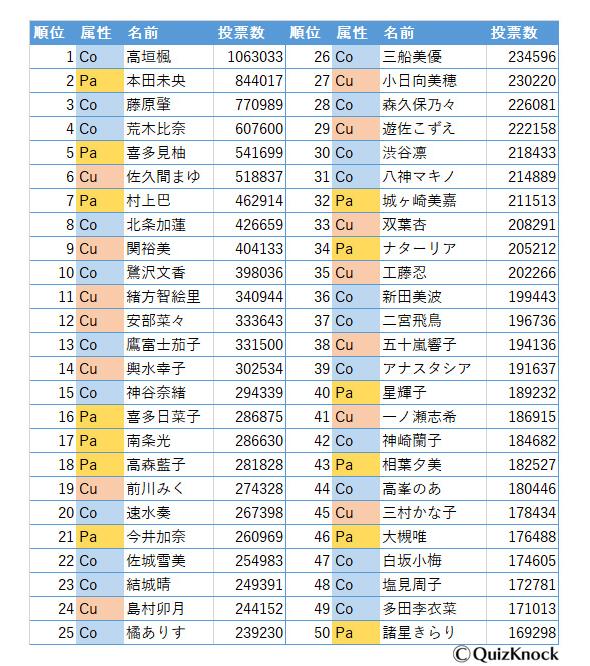
《偶像大師灰姑娘》第6次總選舉的冠軍是高垣楓,以106萬的高票最終問鼎第一位
而在官方公佈的數據中,只有全榜Top 10角色與三種屬性角色分榜的Top 5角色公開具體票數,而投票的總票數沒有任何官方數據發表,於是日本就有人以官方現有的公開數據與對數方程來進行測算
因為灰姑娘的總選舉是每天登陸遊戲就能獲得一張投票券,就算是不課金在投票期間參加活動也能拿到200-300票,所以最後每個偶像的得票數不代表投票實際人數
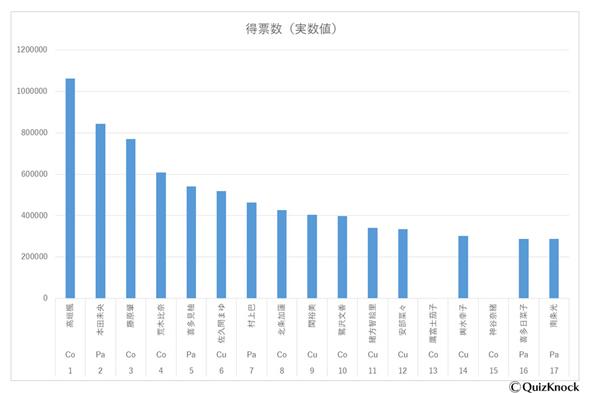
官方公開的原始數據
對數線性回歸
換算出的 y 與 x 方程
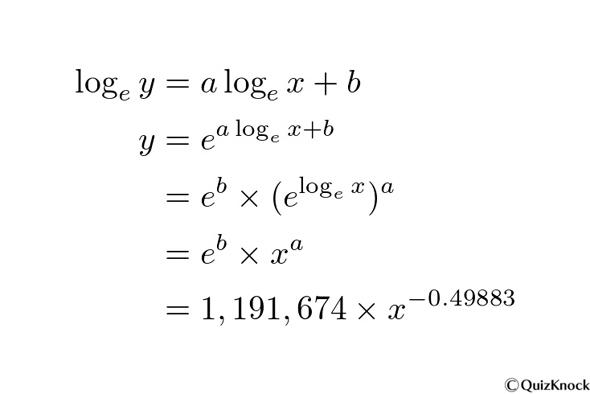

推測中的各偶像得票數
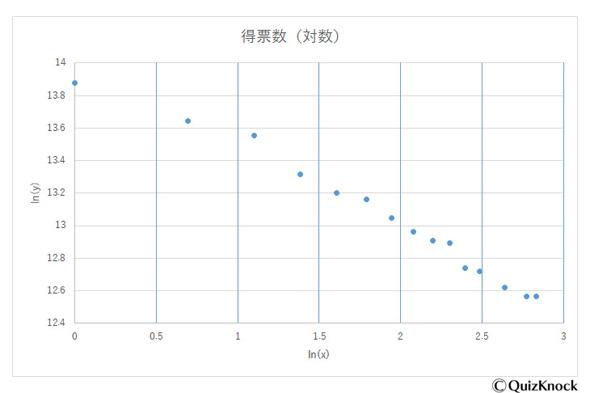
要推測全部183名偶像得票數據,需要先做對數線性回歸分析,以角色得票數為y,排位為x,製作以自然常數e為底的ln(x)、ln(y)的分佈圖
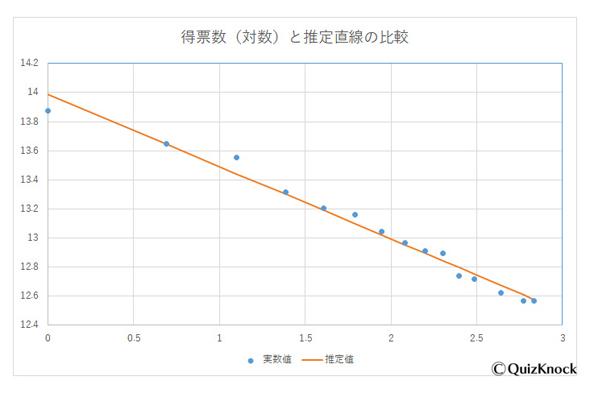
再以最小二乘法計算對數線性回歸方程y=ax+b (y 為lny,x 為lnx)的系數a與常數b,a=-0.49883,b=13.9908,可以得出對數線性回歸方程為ln(y) =-0.49883ln(x)+13.9908,最後換算出y與x的對應方程
根據得到的公式可以推測出最末尾的第183位偶像得票數為88627票,投票總數為3064萬0254票
對數正態分佈
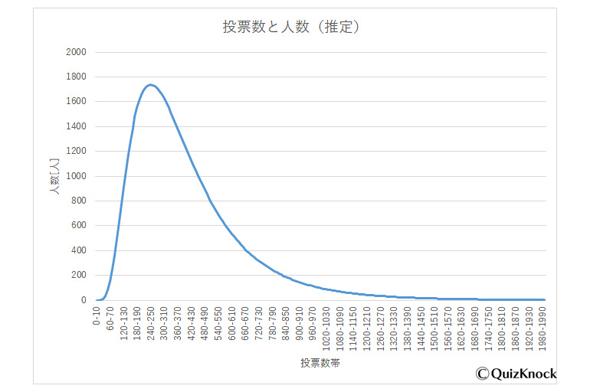
而這些票數有無課金玩家的投票也有課金玩家的投票,課金玩家手裡的票數會比無課玩家多很多
根據網上公開的數據假定在第6次總選舉投票期間灰姑娘遊戲中的活躍玩家數量為75000人,又可以根據這裡的數據作投票數與玩家人數關係的對數正態分佈
以投票數/500作為變量x,x在0到4的範圍內累積值為0.9987,相當於99.87%的數據落在這個範圍中,也就是99.87%的玩家投票數在0-2000票
對數正態分佈的μ=-0.3537、標準差 σ=0.58,投票玩家人數75000人的話總票數為3054萬票,與上面透過角色排位與角色得票數推算出的總票數數據十分接近
根據第6次選舉的數據,灰姑娘女孩一位偶像進入Top 50需要至少17萬票,最末位的第183位偶像有著將近9萬票,所以對於不在Top 50內的偶像來說理論上最多只要再多拿8萬票,就可以在第7次總選舉中殺入Top 50
而根據投票數和人數的正態分佈,灰姑娘玩家中個人投票1000票以上的玩家約為2500名,在75000名投票玩家中佔比為3.3%,但是這2500名玩家投入的票數佔總票數的10%
所以灰姑娘的投票情況是「3%的重課玩家決定10%的票數,97%的無課和微課玩家決定90%的票數」
因此要想讓你的偶像進入Top 50,在現有的基礎上找到40名投票券有2000張的重課玩家,或者找到400名每人手裡有200張投票券的普通玩家,並且確保之前的票數不流失不分散就能在第七次總選舉Top 50看到你的偶像了
原文出處:
http://nlab.itmedia.co.jp/nl/articles/1706/04/news008.html